Hackenbush

4th January 2015

This month we've added Hackenbush to Pencil and Paper Games. It's an appealing game in which one player draws a picture consisting of dots joined by edges. Part of the picture should stand on the ground, represented by a dashed line; for example:

The players then take turns in deleting an edge. Any other parts of the picture that are no longer attached to the ground fall off, and are also deleted.

If you're playing with pencil and paper, cross out an edge to delete it, and then cross out any unattached parts. If you're playing on a whiteboard or blackboard you can rub out the deleted parts.

The last player able to move wins.

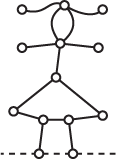
Sample game

Here's a sample game. The second player, Red, has the last move and so wins:

Winning at Hackenbush

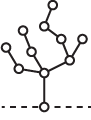
If we choose a simple drawing, consisting of two or more stalks of different lengths, it's clear that this is equivalent to a position in Nim, in which each pile contains the same number of counters as the corresponding stalk has edges:

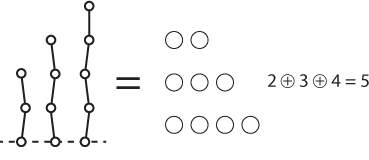
To win in Hackenbush with this drawing we find the Nim sum of the stalks. If it's zero, there's no winning move; otherwise we find a move that makes it zero. For an explanation of how to do this read Nim Strategy.

Here the Nim sum of the position is 5 (where the + in a circle means Nim-sum). Try finding the winning move that makes the Nim sum of the stalks zero; the answer is given at the end of the article.

Hackenbush = Nim

In fact it turns out that every Hackenbush drawing, however complicated, can be simplified to an equivalent drawing consisting of one or more stalks. The winning move is then the one that leads to a position with a zero Nim-sum. In a simple position the winning move is usually obvious. In a more complicated position you may have to try removing each edge in turn to see which one makes the Nim sum zero.

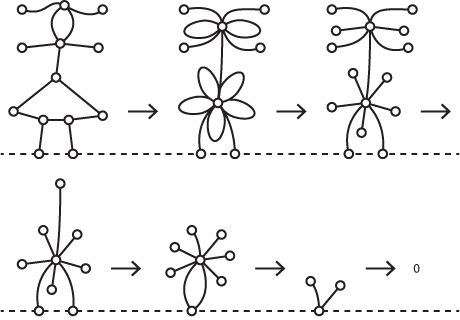
To find the Nim-sum of a Hackenbush picture you can perform three transformations that simplify the picture without affecting its Nim sum.

Simplifying trees

The first transformation simplifies a Hackenbush drawing with branches, like a tree, but no enclosed shapes:

Starting at the highest branching point, replace the branches from that node with a single branch whose length is the Nim sum of the original branches:

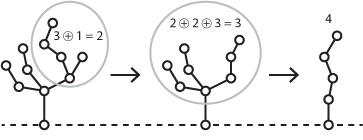
For example, in the first step above we replace the two branches of lengths 3 and 1 with a single branch of length 2.

So the Nim sum of the original tree is 4.

Turning loops into branches

A loop at any node obviously has the same effect as a single branch there. This allows us to find the Nim sum of this flower:

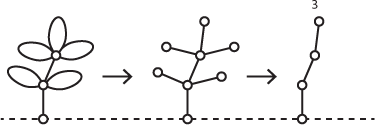
Its Nim sum is 3.

Fusing nodes

If a Hackenbush picture contains an enclosed shape you can fuse all the nodes around that shape, by bringing them together into a single node, without changing its Nim sum.

For example, let's find the Nim sum of the diamond-shaped picture in the first illustration here:

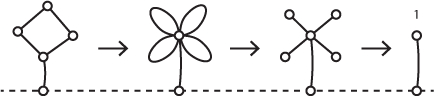
Fusing the four nodes around the diamond makes the flower in the second picture. Then turning the loops into branches we see that the Nim sum is 1.

It's quite difficult to prove why this works; if you're interested see the references here: Hackenbush History.

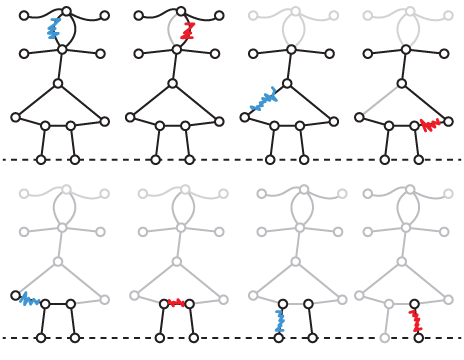
Putting it all together

Finally we can use these three transformations to find the Nim sum of the girl in the original example game above:

Nodes on the ground can be merged without affecting the sum.

In this example the Nim sum is zero, and so there is no winning move for the first player. The best they can do is make a move that leaves the picture as complicated as possible, and hope that the second player can't find a winning move.

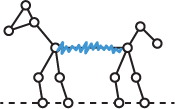
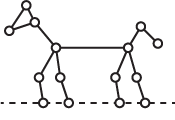
A Hackenbush problem

Finally, as a problem calculate the Nim sum of the dog in the following picture, and then find the winning move:

Answers

Here are the solutions to the two Hackenbush problems given above.

The winning move in the picture of the three stalks is to chop the top off the third stalk:

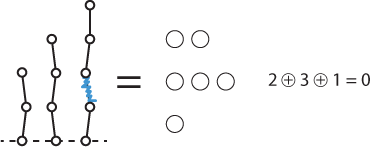
The Nim-sum of the dog is 1, and here's the winning move: